
Üslü Sayılarda Çarpma İşlemi
Üslü sayılarda çarpma işlemi, matematikte önemli bir yer tutar. Bu işlem, benzer tabanlara sahip üslü sayılar arasında yapılırken üslere toplama kuralı uygulanır. Doğru kuralların anlaşılması, hesaplamaların daha hızlı ve etkili bir şekilde gerçekleştirilmesini sağlar.
Üslü Sayılarda Çarpma İşlemi Üslü sayılar, matematikte çok önemli bir yere sahip olan ve sayıların tekrar tekrar çarpımını ifade eden bir kavramdır. Bu çalışmada, üslü sayılar arasındaki çarpma işlemi detaylı bir şekilde ele alınacaktır. Üslü sayılarda çarpma işlemi, temel matematiksel prensipler doğrultusunda gerçekleştirildiğinde, oldukça basit ve etkili bir yöntem sunmaktadır. Üslü Sayıların Tanımı Üslü sayılar, bir sayının kendisiyle belirli bir sayı kadar çarpılmasıyla elde edilen ifadelerdir. Matematiksel olarak, a^n şeklinde gösterilir; burada a, taban sayısını, n ise üssü temsil etmektedir. Örneğin, 2^3 ifadesi, 2 sayısının kendisiyle 3 kez çarpımını ifade eder: 2 × 2 × 2 = 8. Çarpma İşleminde Üslü Sayıların Kullanımı Üslü sayılar arasında çarpma işlemi gerçekleştirilirken, aşağıdaki temel kural uygulanır:
Bu durumda, tabanlar aynı olduğunda, üslere toplama işlemi uygulanır. Örneğin:- 3^2 × 3^4 = 3^(2+4) = 3^6 = 729Bu kuralın anlaşılması, üslü sayılarda çarpma işleminin hızlı ve etkili bir şekilde yapılabilmesi için oldukça önemlidir. Örnekler Üzerinden Açıklama Üslü sayılarla çarpma işleminin uygulanabilirliğini daha iyi anlamak için birkaç örnek inceleyelim:
Bu örneklerde görüldüğü üzere, tabanların aynı olması durumunda, üslere toplama işlemi uygulanarak sonuç elde edilmektedir. Üslü Sayılar Arasında Çarpma İşleminin Genel Özellikleri Üslü sayılarla çarpma işlemi sırasında dikkat edilmesi gereken bazı genel özellikler bulunmaktadır:
Örneğin, 2^3 × 3^2 işlemi, tabanlar farklı olduğu için doğrudan çarpılarak şu şekilde hesaplanabilir:- 2^3 = 8 ve 3^2 = 9- 8 × 9 = 72Bu durumda, sonuç üslü biçimde ifade edilemez. Çarpma İşleminin Uygulama Alanları Üslü sayılarla çarpma işlemi, birçok matematiksel ve bilimsel uygulamada kullanılmaktadır. Özellikle;
gibi birçok alanda büyük öneme sahiptir. Sonuç Sonuç olarak, üslü sayılarda çarpma işlemi, matematiksel yetkinliğin geliştirilmesi için kritik bir konudur. Bu işlemin kuralları ve uygulama alanları, çeşitli disiplinlerde önemli bir rol oynamaktadır. Üslü sayılarla yapılan işlemler, karmaşık hesaplamaların basit bir şekilde yapılmasını sağlayarak, matematiğin temel yapı taşlarından birini oluşturmaktadır. Bu nedenle, üslü sayılar ve çarpma işlemi konularının iyi bir şekilde anlaşılması, matematiksel becerilerin geliştirilmesi açısından önemlidir. |
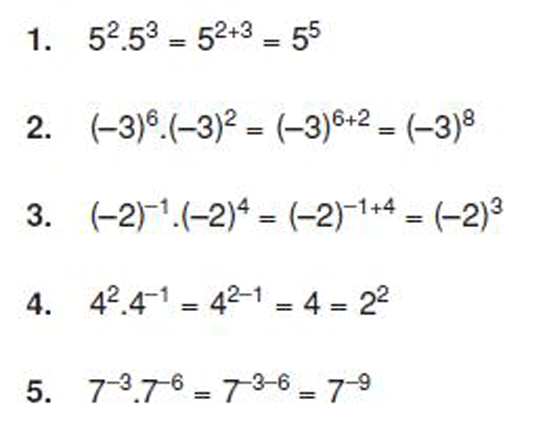






.webp)






.webp)



5 üssü üç +2 üssü yedi sonuç kaçtır
İşlem Adımları
Öncelikle işlemi sırayla yapalım:
5 üssü 3 işlemi:
5^3 = 5 5 5 = 125
Sonra +2 üssü 7 işlemi:
2^7 = 2 2 2 2 2 2 2 = 128
Şimdi bu iki sonucu toplayalım:
125 + 128 = 253
Sonuç
İşlemin sonucu 253'tür.
Peki taban ve üs eşitse ne yapılır?
Eğerli Anonim,
Bu durumda taban ve üs aynı olduğunda sonuç her zaman 1 olur. Örneğin, 5^5 veya 7^7 gibi.